複利和你想的不一樣?完整模擬回測股票、ETF實務上長期的複利效果
相信很多人都修過投資學,或者在開始進入投資市場時學過複利,最常看到的說法就是時間是複利的好朋友、投資要趁早,同樣的本金,早投資給幾年就會...,之類的說法
先用自己網站上的【複利計算機-包含定期定額】,看一下 10% 的報酬率,投資 30 年會有什麼的結果
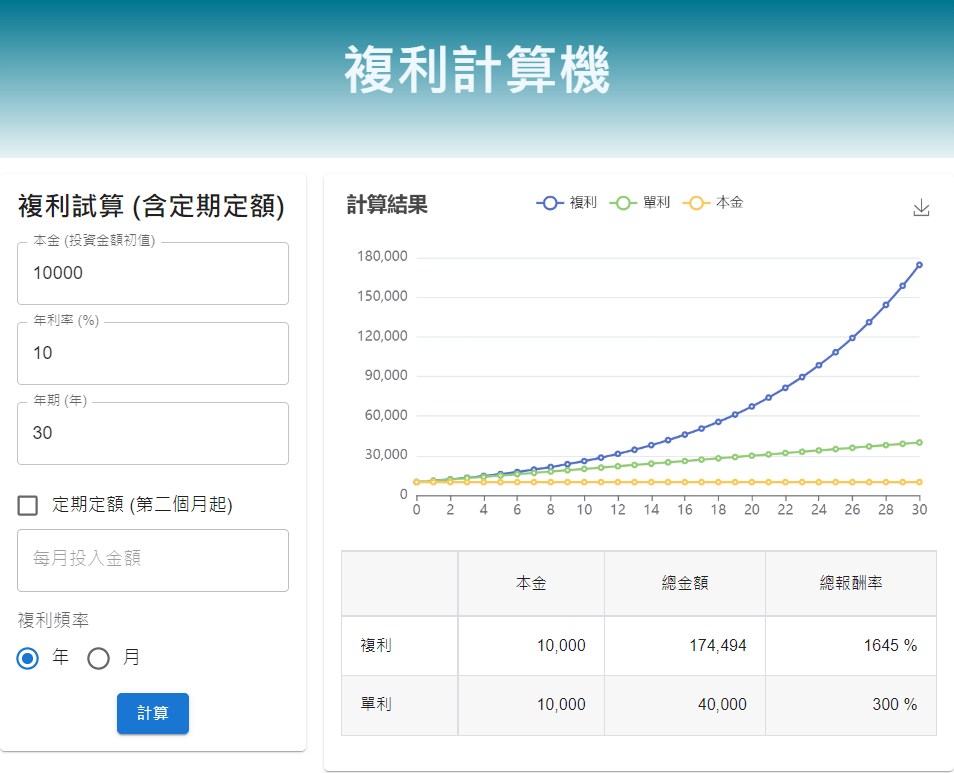
看似很美好,但真的進入投資市場後,發現好像不是那麼回事,理論和實務上到底有多少差距?造成的原因是什麼?還是我們念的理論根本上有問題?
複利和你想的不一樣?
這是我們理想中符合複利表的投資標的走勢
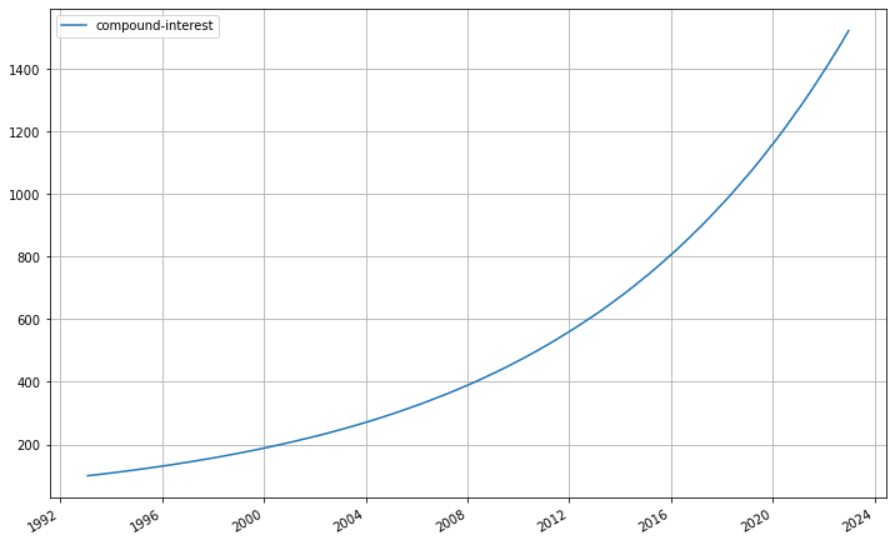
這才是現實中的投資標的走勢
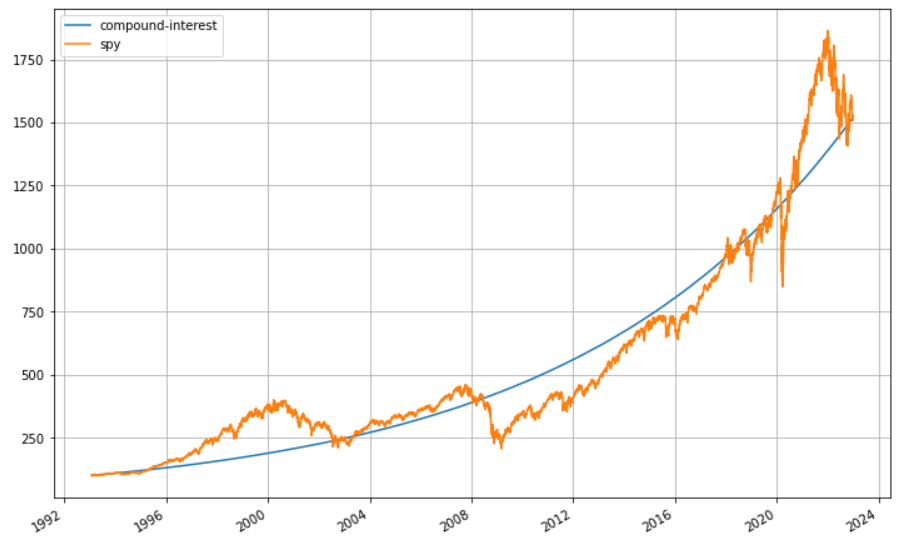
很好懂,簡單的說,股市不會只漲不跌,所以複利表中的複利效果在股市中不會完全成立,也不太需要賣關子,上圖橘線是大家熟悉的 SPY (S&P 500 ETF) 30年的走勢圖,
這樣的走勢大家應該還算可以接受,但如果是下圖呢?
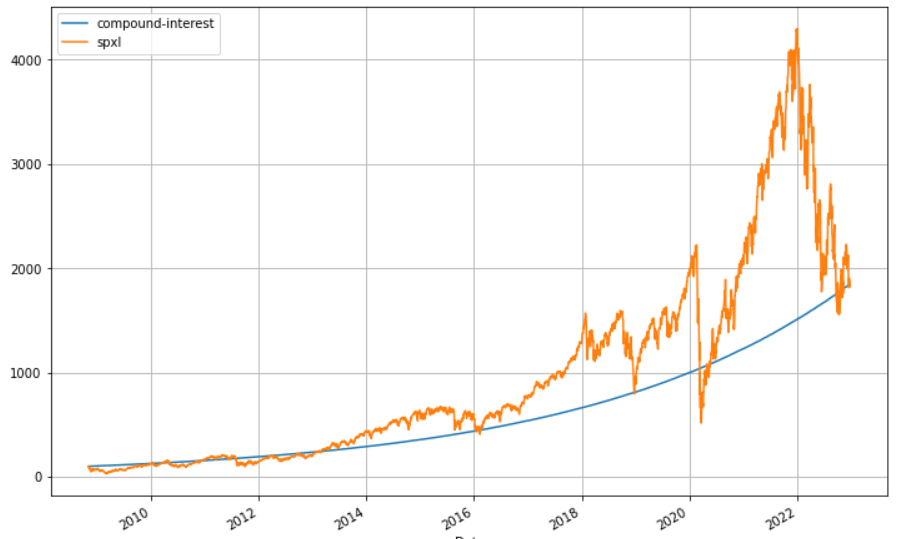
理想和現實 差別在哪裏?
我們先看一下 ffn 報表中 SPY 和 單純複利,回測時間 1993-01-29 ~ 2022-12-23 (約 30 年)
| 總報酬率 | 最大虧損 | CAGR | 年化報酬率(Daily) | 年化波動率(Daily) | |
|---|---|---|---|---|---|
| SPY | 1418.39% | -55.19% | 9.53% | 10.90% | 18.93% |
| 複利 | 1418.39% | 0 | 9.53% | 9.10% | 0 |
這裏看的是 Daily,先有幾個基本的認識
- 理想中的複利最大虧損為 0,因為只會漲不會跌,不會虧損
- 理想中的複利的波動為 0,因為每天的漲幅都一樣
蒙地卡羅模擬股價
蒙地卡羅方法是什麼
蒙地卡羅方法(Monte Carlo method),聽起來好像很專業的名詞,但原理很簡單,就是基於大數法則,透過大量隨機亂數的實驗,當實驗的次數愈多,它的平均值或中位數就會愈趨近於理論值
蒙地卡羅模擬股價公式
我們參考雷大的這篇文章:【如何用蒙地卡羅模擬股價?】,取得 python 的公式如下
S1 = S0 * np.exp((mu - 0.5 *Std**2)*dt + Std*np.sqrt(dt)*np.random.standard_normal())
mu : 資產年化報酬率
Std : 資產年化波動率
dt : 1/252. #模擬路徑為每天,每天經過 1/252 年
S1:明天的股價
S0:今天的股價
實際模擬 SPY 股價 30 年報酬
在使用之前當然需要先驗證,驗證的對象就拿剛才的 SPY,因為我打算模擬 30 年,然後迴圈跑 10000 次, 為了不虐待我的電腦,所以模擬路徑改為「月」,年化報酬率和年化波動率也改為 Monthly,以下為 SPY 的資料
mu : 資產年化報酬率 = 10.26%
Std : 資產年化波動率 = 14.96%
dt : 1/12. #模擬路徑為每月,每月經過 1/12 年
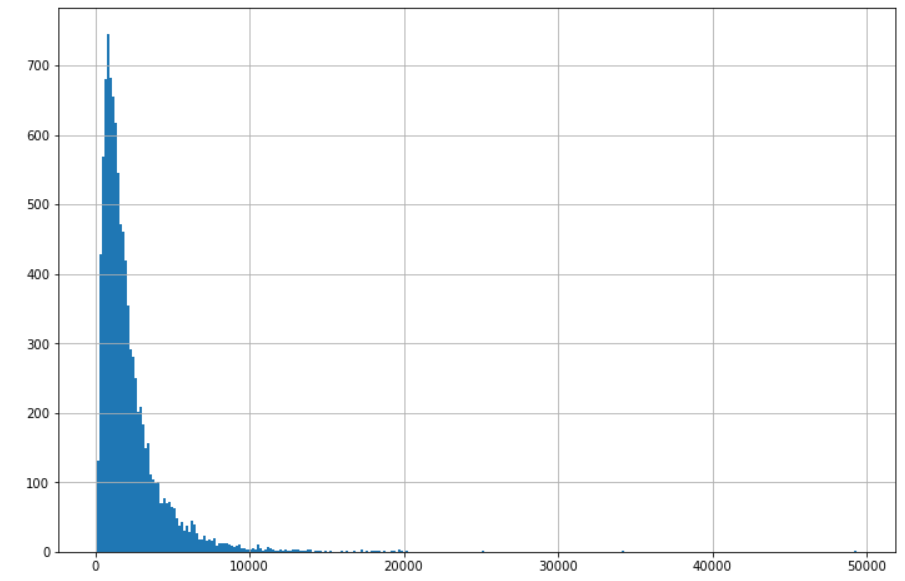
本金用 100,結果如下:模擬結果散佈圖:X 軸為報酬,Y 軸為發生的次數
| 模擬次數 | 報酬平均值 | 報酬最小值 | 報酬中位數 | 報酬�最大值 |
|---|---|---|---|---|
| 10000 | 2153 | 84 | 1542 | 49390 |
先有個概念,這個模擬平均值是沒有意義的,看散佈圖就知道,這是個很明顯的右偏態,平均值會因為某些特別高的值(max 為 49390, 為中位數的 32 倍)一起加下去平均而被高估,就像我和郭台銘平均一人有30億美元的資產一樣,中位數是比較值得參考的數據
SPY 實際的數值為 1518 (CAGR: 9.53%),和模擬的中位數 1542 很接近,代表這個蒙地卡羅模擬股價有一定的參考性在,那我們就開始用這個公式來模擬股價了
CAGR 是什麼
CAGR (compound annual growth rate),中文譯為「複合年均成長率」, 在報表中是年化報酬率的一種,計算的依據只看投資金額的初值和最終值,不考慮中間的波動。
它其實比較接近現實中大家認知的真正報酬率,就是期初投入多少錢,期末真的能拿到手金額的年化報酬。
這個網站有提供【CAGR 年化報酬率計算機】
模擬同樣年化報酬率(10%),不同波動率的結果
波動率先分別用 5%,10%,20%,40% 來比較一下結果
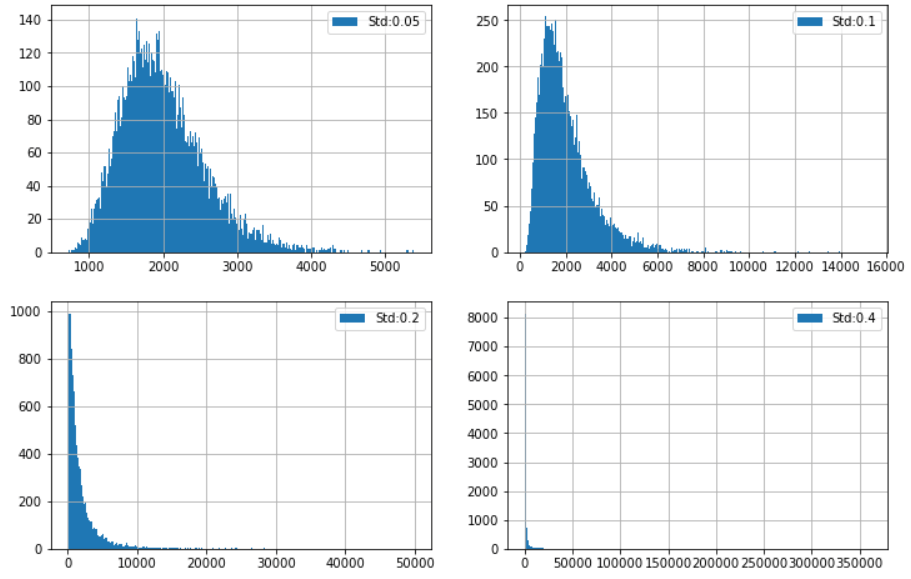
模擬結果散佈圖:X 軸為報酬,Y 軸為發生的次數
| 波動�率 | 本金 | 30年報酬中位數 | CAGR |
|---|---|---|---|
| 5% | 100 | 1922 | 10.35% |
| 10% | 100 | 1735 | 9.98% |
| 20% | 100 | 1086 | 8.27% |
| 40% | 100 | 172 | 1.82% |
這個圖表很明顯,波動愈大,右偏愈嚴重,報酬的中位數愈低,以 40% 波動的模擬,甚至 CAGR 低到 1.82%
還是得虐待電腦,這次同樣用 10% 年報酬率,然後波動率從 2%, 4%, 6% 一直跑迴圈算到 50%,整理繪圖如下
藍線為理想中的複利報酬 10%,綠線為使用蒙地卡羅的 CAGR 模擬結果,Y 軸為報酬率,X 軸為波動率 (小提示,將滑鼠移到圖形上可以看到數據)
- 這張圖就更明確了,波動愈大,蒙地卡羅模擬出來的 CAGR 愈低,甚至在波動率到 45% 的時候,CAGR 變成了負值,代表你的投資經過了 30 年,結果最後的金額會比本金還少
夏普值 是什麼
夏普值 (Sharpe Ratio) = 報酬率 / 波動率
模擬同樣夏普值(0.6),不同波動率的結果
為什麼要用同樣的夏普值來做模擬?今年年初寫過一篇文章:【槓桿型 ETF 適不適合長期持有?回測 TQQQ】,文章中的槓桿型 ETF 就是同時放大報酬和波動,下面的回測數據可以看出同時放大報酬和波動後長期持有的真正報酬��率
使用 0.6 是因為 SPY 30 年的夏普值約在 0.6,繼續虐待電腦,這次的模擬從 2%, 4%, 6% 一直跑迴圈算到 80%,整理繪圖如下
藍線為理想中的複利報酬,綠線為使用蒙地卡羅的 CAGR 模擬結果,Y 軸為報酬率,X 軸為波動率 (小提示,將滑鼠移到圖形上可以看到數據)
- 從這張圖來看,在波動率 20% 以下時,理想值和模擬實際值很接近,但隨著波動率的增加,模擬實際值並沒有跟上理想值
- 波動率在 40% 左右,模擬實際值幾乎不再上升,甚至在 70% 左右反而開始下降
在【槓桿型 ETF 適不適合長期持有?回測 TQQQ】這篇文章中的 Mock TQQQ 23 年的總報酬率是跑輸 QQQ 的,當初覺得有點驚訝,但從 Mock TQQQ 當時測的波動率高達 78% 來看,用這個數學模型解釋就一點都不奇怪了
不同投資商品的 報酬率、波動率 分佈圖
講了那麼多報酬率和波動率,所以我們經常投資的商品的報酬率和波動率到底是多少?
簡單整理了一下比較常見的一些股票型 ETF、債券 ETF、股票如下圖 (小提示,將滑鼠移到圖形上可以看到數據), 數據回測時間除了 TLSA 外均為 2008-06-26(VT 的上市時間) 到 2022-12-27,TSLA 則是它上市時間到 2022-12-27,這個值會隨回測的時間不一樣而不同,所以儘量讓大家的時間都差不多
- 也不意外,債券型 ETF 多是低波動低報酬,股票型 ETF 次之,個股尤其是科技股就比較多高波動高報酬
- ��從剛才的模擬大概在 40% 的波動率可以得到最佳的報酬,以大盤型 ETF 大概是兩倍槓桿左右,科技股則沒什麼開槓桿的空間了
結論
依慣例,文章太長,整理一下重點
- 複利表中的複利效果在股市中不會完全成立,因為複利表中的複利波動為0,只漲不跌且漲幅相等,在股市不成立
- 影響複利效果的原因在於報酬率和波動率
- 使用蒙地卡羅摸擬股價結果:波動率愈大,右偏態愈明顯,中位數愈低,代表實務投資狀況波動率愈高的投資標的,在長期投資實際的報酬會愈容易不符預期
- 開槓桿投資即使報酬率預期為正值,長期投資的報酬率並不會隨槓桿倍數增加,反倒是波動率過高時報酬率還容易反而下降
- 大盤型 ETF 的最佳報酬大概是兩倍槓桿左右,科技股則沒什麼開槓桿的空間
備註
- 同樣我將蒙地卡羅摸擬股價的程式放在 Colab,【Colab 連結】,不過迴圈次數只有 1000 次,請自行加大和改報酬率、波動率, 如果不知道 Colab 怎麼使用,可以參考【Google Colab(Colaboratory) 簡易教學】這篇文章
- 網站提供財務工具【複利計算機-包含定期定額】、【CAGR 年化報酬率計算機】,歡迎使用和分享
- 此資料僅為站長自行模擬回測,不為未來投�資獲利之保證。【免責聲明】
